監督スクリプトを記述しよう
このページでは、前回に引き続き、ゲームの監督スクリプトを記述していきます。監督スクリプトの主なお仕事は以下のような感じでしたね。
・ゲーム開始直後、数球オブジェクトを初期配置に並べる
・自分のターンにて、パワーや方向などを調節し、手球を発射
・CPUが（とあるルールにのっとり）パワーや方向などを調節し、手球を発射
・発射後、手球や数球の状況によって、次の番が自分かCPUかを決定する
前回と前々回で、二つ目の自ターン時の処理作業までスクリプト化完了しました。今回は三つ目の、CPUターン時の処理作業をスクリプト化していきましょう！
スクリプトを書こう３（CPUターンの動き）
今回はUpdateメソッド中の、myturn=1、waittime=0、つまりCPUの番での処理を書いていきます。↑の変数にピンと来ない方は、制作手順２－２のページ前半で、Updateメソッドの全容を紹介していますので、まずはそちらをご確認下さい。m(_ _)m
CPUの動きについて（概要）
ゲームが遊べるページに白黒反転して書いてある内容を以下に引用します。そのままでは見辛い(笑)ので、ここでは黒字に戻します。
今回のCPUは、次狙うべき数球に直接当てに行きます。それだけです！(笑)
間にジャマな数球が入っていようが、お構いなしに狙いの球を直接狙ってきます。これだけ聞くとアホの子ですが、これ位シンプルな挙動でも結構強いので、油断せず頑張って下さい！
また、直前でプレーヤーがファールした場合、ちゃんとCPUは狙いの数球の直近に手球を配置してきます。そのターンはほぼ確実に入れて来ますので、あまりファールはやらないように…。
概要はこんな具合です。今回は、↑の言葉を再現出来るように、スクリプトを書いていきます。前回と前々回で、自ターンのスクリプトを書いた時と同様、とりあえずざっくりスクリプト全体を書いてみると、こんな具合でしょうか。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
//相手の番 if (this.myturn == 1 && this.waittime == 0){ if (this.readyswitch == 0){ this.readyswitch = 1; beforeturn(); //初期設定もろもろ <制作手順２－２参照> //CPUの手球位置調整（手球移動可能な場合） if (this.canmove == 0){ //【要追加】①目標数球のすぐ横に設置 } //【要追加】②CPUの方向調整 changeorder(100, this.relangle2); //左上の表示変更 <制作手順２－２参照> } //発射まで2秒待ち this.delta += Time.deltaTime; if (this.delta > 2.0f) { this.delta = 0f; beforeshot(); //手球発射前の準備 <制作手順２－３参照> //手球発射！…player_ballスクリプト中のメソッドを使用 <制作手順３参照> this.player_ball.GetComponent<player_ball>().start_shot(this.shotpower,this.shotangle); } } |
ちなみに、コメント行に<制作手順２－□参照>と書いてある行は、前回と前々回自ターンのスクリプト作成時に作ったメソッド・スクリプトが使い回し出来る部分になります！前回まで頑張って色々細かいスクリプトを作った甲斐がありました…（感動）。
という訳で、コメント行に【要追加】となっている行が、今回新規にスクリプト詳細を考えていく部分になります。大きく分けて２つありますので、順番にスクリプト化していきましょう！
①CPUの番で手球移動可能な場合、目標数球のすぐ横に設置
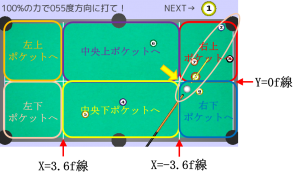所謂canmove=0の場合、手球はどこにでも動かせるので、CPUは狙う数球の真横に配置したいのですが、折角なので右図の黄色矢印のように、ポケットに直接落とせるような向きに配置します。さらに右図のように狙う数球の位置によって、どのポケットに入れるかも変えていきます。その辺を考慮したスクリプトがコチラ。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
//以下はStartメソッドに追加 //各ポケットオブジェクト this.hole_ur = GameObject.Find("hole_ur"); this.hole_lr = GameObject.Find("hole_lr"); this.hole_uc = GameObject.Find("hole_uc"); this.hole_lc = GameObject.Find("hole_lc"); this.hole_ul = GameObject.Find("hole_ul"); this.hole_ll = GameObject.Find("hole_ll"); //以下、別メソッド void setCPUball(){ //CPUがplayerballの位置を自由配置出来る際の置き方 //目標数球の位置によって狙う穴の位置を変更する Vector3 targetpos = this.number_balls[this.remaininglist[0] - 1].transform.position; Vector3 shotvec = new Vector3(1.0f, 0f, 0f); Vector3 shotvec2 = new Vector3(1.0f, 0f, 0f); if (targetpos.x < -3.6f && targetpos.y >= 0f){ //画面中右上に目標数球がある時は、右上穴を狙って打つ shotvec = this.hole_ur.transform.position - targetpos; shotvec2 = shotvec / shotvec.magnitude; } else if (targetpos.x < -3.6f && targetpos.y < 0f){ //画面中右下に目標数球がある時は、右下穴を狙って打つ shotvec = this.hole_lr.transform.position - targetpos; shotvec2 = shotvec / shotvec.magnitude; } else if (Mathf.Abs(targetpos.x) <= 3.6f && targetpos.y >= 0f){ //画面中中央上に目標数球がある時は、中央上穴を狙って打つ shotvec = this.hole_uc.transform.position - targetpos; shotvec2 = shotvec / shotvec.magnitude; } else if (Mathf.Abs(targetpos.x) <= 3.6f && targetpos.y < 0f){ //画面中中央下に目標数球がある時は、中央下穴を狙って打つ shotvec = this.hole_lc.transform.position - targetpos; shotvec2 = shotvec / shotvec.magnitude; } else if (targetpos.x > 3.6f && targetpos.y >= 0f){ //画面中左上に目標数球がある時は、左上穴を狙って打つ shotvec = this.hole_ul.transform.position - targetpos; shotvec2 = shotvec / shotvec.magnitude; } else if (targetpos.x > 3.6f && targetpos.y < 0f){ //画面中左下に目標数球がある時は、左下穴を狙って打つ shotvec = this.hole_ll.transform.position - targetpos; shotvec2 = shotvec / shotvec.magnitude; } this.player_ball.transform.position = targetpos - shotvec2; this.cue.transform.position = targetpos - shotvec2; } |
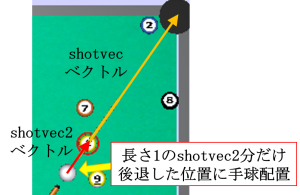「shotvec2 = shotvec / shotvec.magnitude;」というスクリプトで、shotvec ベクトルから、向きはそのままで、長さが１になるようなベクトルshotvec2 を生成しています（所謂、単位ベクトルを生成しています）。これにより、手球は右図のように配置されるので、そのまま打てば数球がポケットに入る、という算段になっております。
あと、これは制作手順２－２下の方で解説した話の復習になりますが、remaininglist[0]は残っている数球の最小番号でしたので、this.number_balls[this.remaininglist[0] - 1]は数球の最小番号オブジェクトを指します。つまり、狙う数球オブジェクトを指していますね。
②CPUの方向調整
方向調整については、引用文中にもあるように、目標数球の間に邪魔者があろうが関係なく、直接狙いの数球に照準を合わせます。CPUのアルゴリズムとしては、一番単純な仕組みになりますが、スクリプトに書き下すとこんな感じです。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
//Updateメソッド中…CPUの方向調整 //手球から目標数球に向けたベクトル this.relpos = this.number_balls[this.remaininglist[0] - 1].transform.position - this.player_ball.transform.position; //上で求めたベクトルと真右方向（基準方向）間の角度を計測 this.relangle = Vector3.Angle(-Vector3.right, this.relpos); if (this.relpos.y != 0f) { //角度に符号を追加（relpos.y>0なら+の角度、relpos.y<0なら-の角度） this.relangle = this.relangle * this.relpos.y / Mathf.Abs(this.relpos.y); } this.relangle2 = Mathf.RoundToInt(this.relangle); //左上に表示する用 this.cue.transform.rotation = Quaternion.Euler(0, 0, -this.relangle); |
Vector3.Angle(２つのベクトル)により、２つのベクトル間の角度を求められます。ただし、求められる角度は絶対値（±符号なし）で出て来ますので、反時計（+の角度）？時計（-の角度）？どちら向きの角度なのかが分かりません。よって、次の行でrelpos.yの符号（=(relpos.y)/(relpos.yの絶対値)で求めています）を角度情報に追加して、角度の向きを確定させています。
最後に
今回は、CPUターンの挙動について、Updateメソッド中にスクリプトを書いていきました。次回は、止まるまで待ち＆次はどちらの番になるかの処理について、スクリプト化していきます！！監督スクリプトはもう少しで完成です！